|
Click Soundfile 1.18. You’ll hear composer Warren Burt’s piece for tuning forks, "Improvisation in Two Ancient Greek Modes."
Now, why do tuning fork functions have their simple, sinusoidal shape? Think about how the tip of the tuning fork is moving over time. We see that it is moving back and forth, from its greatest displacement in one direction all the way back to just about the same displacement in the opposite direction.
Imagine that you are sitting on the end of the tine (hold on tight!). When you move to the left, that will be a negative displacement; and when you move to the right, that will be a positive displacement. Once again, as time progresses we can graph the function that at each moment in time outputs your position. Your back-and-forth motion yields the functions many of you remember from trigonometry: sines and cosines.
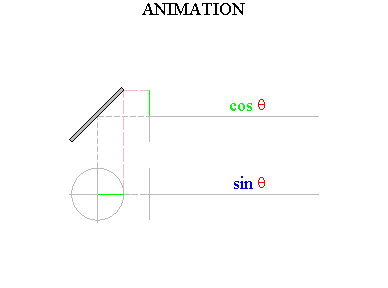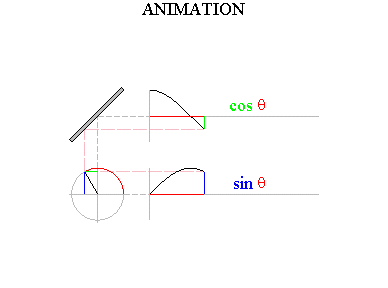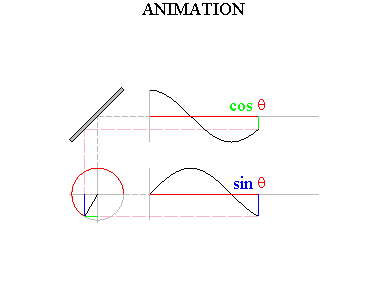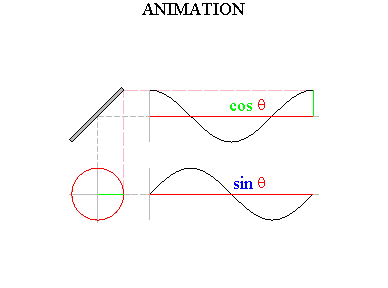
Figure 1.21 Sine and cosine
waves. Thanks to Wayne Mathews for this image.
Any sound can be represented as a combination of different amounts of these sines and cosines of varying frequencies. The mathematical topic that explains sounds and other wave phenomena is called Fourier analysis, named after its discoverer, the great 18th century mathematician Jean Baptiste Joseph Fourier.
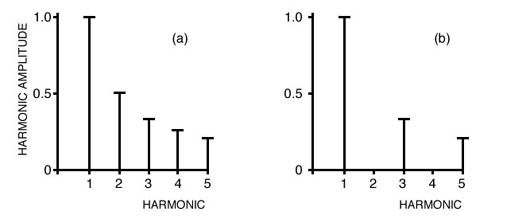
Figure 1.22 Spectra of (a) sawtooth
wave and (b) square wave.
Figure 1.22 shows the relative amplitudes of sinusoidal components of simple waveforms.
For example, Figure 1.22(a) indicates that a sawtooth wave can be made by addition in the following way: one part of a sine wave at the fundamental frequency (say, 1 Hz), then half as much of a sine wave at 2 Hz, and a third as much at 3 Hz, and so on, infinitely.
In Section 4.2, we’ll talk about using the Fourier technique in synthesizing sound, called additive synthesis. If you want to jump ahead a bit, try the applet in Section 4.2, that lets you build simple waveforms from sinusoidal components. Notice that when you try to build a square wave, there are little ripples on the edges of the square. This is called Gibbs ringing, and it has to do with the fact that the sum of any finite number of these decreasing amounts of sine waves of increasing frequency is never exactly a square wave.
What the charts in Figure 1.22 mean is that if you add up all those sinusoids whose frequencies are integer multiples of the fundamental frequency of the sound and whose amplitudes are described in the charts by the heights of the bars, you’ll get the sawtooth and square waves.
This is what Fourier analysis is all about: every periodic waveform (which is the same, more or less, as saying every pitched sound) can be expressed as a sum of sines whose frequencies are integer multiples of the fundamental and whose amplitudes are unknown. The sawtooth and square wave charts in Figure 1.22 are called spectral histograms (they don’t show any evolution over time, since these waveforms are periodic).
These sine waves are sometimes referred to as the spectral components, partials, overtones, or harmonics of a sound, and they are what was thought to be primarily responsible for our sense of timbre. So when we refer to the tenth partial of a timbre, we mean a sinusoid at 10 times the frequency of the sound’s fundamental frequency (but we don’t know its amplitude).
The sounds in some of the following soundfiles are conventional instruments with their attacks lopped off, so that we can hear each instrument as a different periodic waveform and listen to each instrument’s different spectral configurations. Notice that, strangely enough, the clarinet (whose sound wave is a lot like a sawtooth wave) and the flute, without their attacks, are not all that different (in the grand scheme of things).
|

