week3
Links
Code
- G6610 older class
-- this has a good disussion (with purty pictures even!) of
the "fractal reflection" exercise we did in class. Again, some
of the links are a little old... the link to the RTcmix
STEREO
instrument documentation is older, and
use the xmountains.tar.gz package linked below here for
Mac OSX.
- reflect.tar.gz
-- the code for our 'fractal reflection' exercise (described
in the "G6610 older class" link above)
- mandel.tar.gz
-- the Mandelbrot set application, zoom in and realize as a
frequency vs. time graph (decribed briefly below)
- xmountains.tar.gz
-- Mac OSX (under X11.app) version of the fractal mountain-making
program. I think this will also compile ok on Linux "as is",
otherwise visit the "G6610 older class" link above for the
Linux version.
The first thing we did in class was to play some examples of Real Live
Fractal Music, which did indeed sound very fractal indeed it
did sound very very fractal indeed it sounded very very very very fractal
indeed it did indeed sound very very very very very very very very fractal...
One thing to keep in mind with a lot of these algorithmic topics is that
many of them are related. For example, when we discuss L-systems later
in the term, they are often seen as a good example of a procedure which
can generate a fractal boundary (basically a fractal has a 'fractional
dimension' as defined by Benoit Mandebrot in his class book The
Fractal Geomtery of Nature -- a "wiggliness" that causes the boundary
to lie between two dicrete measure of dimension. For example, an infinitely
crinkled line can't really be thought of as lying entirely in 1 dimension,
but it really isn't a 2-dimensional object either; a fractal).
Reflections from a Fractal Boundary
Instead of using fractal techniques to control an unfolding melodic line
(as in many of the fractal music examples), we explored the use of
fractal data in another area -- the creation of time-delay values
to simulate the reflection of sound from an invented mountain or canyon
wall. The
G6610 older class
web page has a good explanation of what we did, complete with goofy pictures
of sound bouncing from a fake-looking fractal boundary.
Interpreting the Mandelbrot Set

Next we looked at a simple little application that graphed the
Mandelbrot set (shown in basic form above). The Mandelbrot set
is generated using the simple-looking equation
The hidden trickiness comes from the fact that z and
c are complex variables containing two components, a
real and an imaginary part. The graph above was plotted by interpreting
the real and imaginary components as x and y dimensions for the plot.
The set is created by iterating the above equation a number of times.
the values of z will do one of two things: the iterated
output of the equation will bounce around inside the Mandelbrot
set boundary (the blue part above), or the output will eventually
"fly off" to infinity.
We can make a more dramatic-looking graph
by measuring how quickly points outside the Mandelbrot boundary
go to infinity and using this to change the coloring of each initial
point:

Adding the ability to select an "zoom in" to different sections of the
Mandelbrot set (like the
Fractal Microscope) allos us to generate a wide range of different
images:


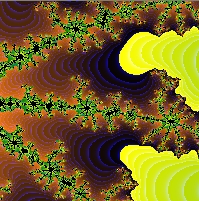
As with the Henon attractor application in
last week's fun, we can interpret
these images as extended frequency/time graphs. The brightness of the
color of each pixel represents the amplitude of the particular frequency
mapped to that pixel row.
Here are several example sounds created by interpreting the horizontal
axis as time (25 second span) and the vertical axis as frequency
(70 Hz -- 2570 Hz):
These were generated using the "mandel2" application. "mandel2"
writes out RTcmix scorefiles to the standard output. Be careful, though,
because this application can generate a very large scorefile.
It will take some time to render, i.e. it won't realize the sound
in real-time.





