week2

We used RTcmix, Max/MSP and showed a JSyn example for our class demos. For the attractor-realization applications, RTcmix was imbedded in a wxWindows graphics context. See the resources web page for appropriate links to these packages.

Code

Here are the source-code files for the class examples:

popeq.sit -- Luke's Max/MSP realization of the "population equation"
lorenz.tar.gz -- development of the Lorenz attractor sonification app
henon.tar.gz -- development of the Henon attractor sonification app

We talked about different ways of "doing" algorithmic composition and demonstrated some simple scorefiles (scripts) to show probabilistic and deterministic approaches (see below). We also looked at times where probabilistic/deterministic techniques overlap -- constrained probabilities and chaotic equations.

Simple Algorithmic Scorefiles

Our first little scorefile showed a very simple 'algorithmic' operation -- creating a scale (both logarithmic and linear). A variant of this deterministic approach uses the bottom part of a simple parabola (y = x²), mapping it into a frequency range we can hear and stepping through the range [-1.0, 1.0] to generate our notes:


rtsetparams(44100, 2)
load ("WAVETABLE")
reset(44100)

makegen(1, 24, 1000, 0,0, 1,1, 2, 0)
makegen(2, 10, 1000, 1.0, 0.3, 0.1)

start = 0

x = -1.0

for (i = 0; i < 20; i = i+ 1)
{
	y = x*x
	pitch = y * 1000.0 + 100.0
	WAVETABLE(start, 0.2, 30000, pitch, 0.5)
	start = start + 0.1
	x = x+0.1
}

Next we explored the use of constrained randomness, ultimately winding up with a little scorefile to create a narrowing/widening effect on our note pitches (the widening was a happy byproduct of sloppy programming -- yay!):


rtsetparams(44100, 2)
load ("WAVETABLE")
reset(44100)

srand(8)

makegen(1, 24, 1000, 0,0, 1,1, 2, 0)
makegen(2, 10, 1000, 1.0, 0.3, 0.1)

start = 0
low = 100
high = 1000

for (i = 0; i < 150; i = i+ 1)
{
	pitch = irand(low, high)
	WAVETABLE(start, 0.2, 10000, pitch, 0.5)
	start = start + 0.03
	low = low+10
	high = high-10
}

Finally, we wrote a simple scorefile that did a fun sort of 'spectral decomposition'. We started by generating the aligned harmonics of a sawtooth waveform. We then gradually randomized the start time of each harmonic, ultimately resulting in a cascading effect through the harmonic spectrum:


rtsetparams(44100, 2)
load ("WAVETABLE")
reset(44100)

makegen(1, 24, 1000, 0,0, 1,1, 5, 0)
makegen(2, 10, 1000, 1.0)

start = 0
pitchbase = 149.78
ampbase = 20000

lo = 0.0
hi = 0.001

for (i = 0; i < 50; i = i+1)
{
	for (j = 1; j < 20; j = j + 1)
	{
		pitch = j*pitchbase
		amp = ampbase * (1/j)
		hstart = start + irand(lo, hi)
		WAVETABLE(hstart, 0.2, amp, pitch, 0.5)
	}
	hi = hi + 0.007
	start = start + 0.2
}

Not content with that, of course we then began to randomize the frequency of each harmonic. What fun:


rtsetparams(44100, 2)
load ("WAVETABLE")
reset(44100)

makegen(1, 24, 1000, 0,0, 1,1, 5, 0)
makegen(2, 10, 1000, 1.0)

start = 0
pitchbase = 149.78
ampbase = 20000

lo = 0.0
hi = 0.001

plo = 0.0
phi = 1.0

for (i = 0; i < 50; i = i+1)
{
	for (j = 1; j < 20; j = j + 1)
	{
		pitch = j*pitchbase
		hpitch = pitch + irand(plo, phi)
		amp = ampbase * (1/j)
		hstart = start + irand(lo, hi)
		WAVETABLE(hstart, 0.2, amp, hpitch, 0.5)
	}
	hi = hi + 0.007
	phi = phi + 2.0
	start = start + 0.2
}

Chaotic Attractors: The Population Equation

The first chaotic equation we tried was the famous "population equation":

x_n = Rx_n-1(1-x_n-1)

This equation was made famous in James Gleick's book Chaos: the Making of a New Science. When plotted by changing the value of R and iterating the equation, we can see regions of relative stability (single or double values are always generated) interspersed with areas of chaotic behaviour:

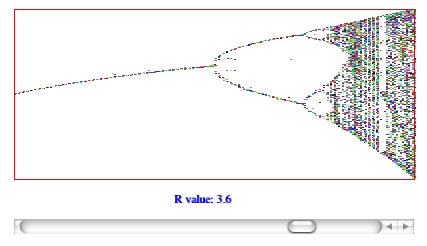
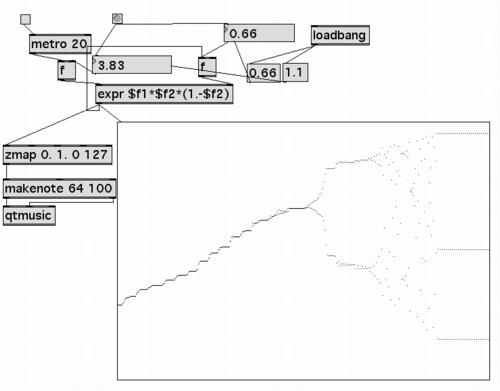
Mapping the output of the equation onto pitch seemed like a logical thing to do, so we did. Luke Dubois has also created a nifty Max/MSP patch that uses this equation (available at the top of this web page):

Chaotic Attractors: The Lorenz Attractor

The Lorenz attractor is generated by iterating the following three differential equations, and plotting x against z after calculating the delta-difference for the points x, y and z:

dx/dt = a(y-x)
dy/dt = bx - y - zx
dz/dt = xy -cz

Because we were always plotting tiny delta-differences in the values of x and z, the graph was nicely connected, and by inserting a small amount of time between each point plotted we could observe the plot as it orbited around one basin of attraction and then jumped into the other (the characteristic behavior of the Lorenz attractor -- originally developed as an atmospheric/climate model). The obvious thing for us computer-musicians to do is to realize this as a graph of frequency vs. amplitude and listen as the merry Lorenz attractor unfolded itself. Oh what fun!

Chaotic Attractors: The Henon Attractor

The Henon attractor presented a slightly different challenge in sonic interpretation. The attractor is generated in a fashion almost as simple as the chaotic population equation described earlier. Simply iterate the following two equations:

x_n = y_n-1 - ax_n-1² + 1
y_n = bx_n-1

Plotting the [x,y] pairs that come from the above will ultimate generate the attractor.

The tricky part is that, like the population equation in one of the chaotic regimes, the points jump randomly along the attractor orbit. If we just played these notes as pitches, then it would sound like random notes.

Instead, we imagined trying to capture the 'essence' of the attractor-filling process, because essence-capturing sure seemed like a good idea at the time. We treated the graph above as a simplified spectral (FFT) plot for a 2-second chunk of time, and repeatedly realized it as we plotted 10 points for each 2-second burst. As the attractor filled in, the initially schematic sound of the swooping attractor gradually became a more coherent musical gesture. Sort of.

There's a whole lot more fun to be had with these algorithmic entities. I think the key to really doing something interesting is to think beyond the simple, straightforward realizations that we made for class demo purposes. Mapping our plots onto frequency (even as spectra) makes a kind of intuitive sense, but surely there is an undiscovered sonic landscape awaiting the creative individual who can imagine even more rewarding uses of these approaches.