Chapter 4: The Synthesis of Sound by Computer

Section 4.5: Amplitude Modulation

Introduction to Modulation

We might be more familiar with the term modulation in relationship to radio. Radio transmission utilizes amplitude modulation (AM) and frequency modulation (FM), but we too can create complex waveforms by using these techniques.

Modulated signals are those that are changed regularly in time, usually by other signals. They can get pretty complicated. For example, modulated signals can modulate other signals! To create a modulated signal, we begin with two or more oscillators (or anything that produces a signal) and combine the output signals of the oscillators in such a way as to modulate the amplitude, frequency, and/or phase of one of the oscillators.

In the amplitude modulation equation, the DC offset (a signal that is essentially a straight line) is added to the signal m(t) and multiplied by a sinusoid with frequency f_c . A_c is the carrier amplitude, and k_a is the modulation index.

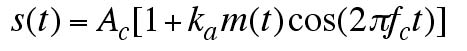
Applet 4.8
LFO modulation

Applet 4.9 shows what happens, in the case of frequency modulation, if the modulating signal is low frequency. In that case, we’ll hear something like vibrato (a regular change in frequency, or perceived pitch). We can also modulate amplitude in this way (tremolo), or even formant frequencies if we want. Low-frequency modulations (that is, modulators that themselves are low-frequency signals) can produce interesting sonic effects.

But for making really complex sounds, we are generally interested in high-frequency modulation. We take two audio frequency signals and multiply them together. More precisely, we start with a carrier oscillator and attach a modulating oscillator to modify and distort the signal that the carrier oscillator puts out. The output of the carrier oscillator can include its original signal and the sidebands or added spectra that are generated by the modulation process.

Amplitude Modulation

Figure 4.13 shows how we might construct a computer music instrument to do amplitude modulation. The two half-ovals are often called unit generators, and they refer to some software device like an oscillator, a mixer, a filter, or an envelope generator that has inputs and outputs and makes and transforms digital signals.

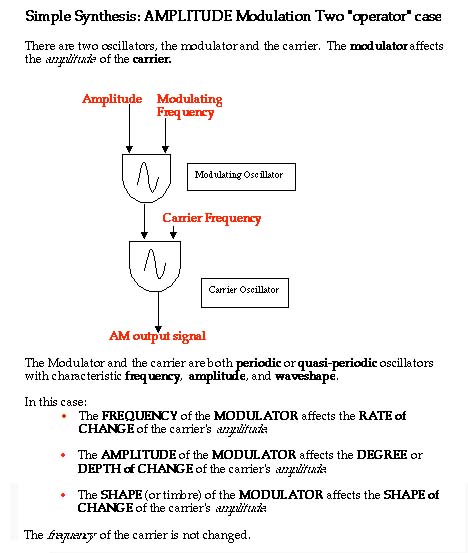
Figure 4.13 Amplitude modulation, two operator case.

A low-pass moving filter that uses a sine wave to control a sweep between 0 Hz and 500 Hz.

Soundfile 4.19
High-pass moving filter (modulated by sine)

A high-pass moving filter that uses a sine wave to control a sweep between 5,000 Hz and 15,000 Hz.

Soundfile 4.20
Low-pass moving filter (modulated by sawtooth)

A low-pass moving filter that uses a sawtooth wave to control a sweep between 0 Hz and 500 Hz.

Soundfile 4.21
High-pass moving filter (modulated by sawtooth)

A high-pass moving filter that uses a sawtooth wave to control a sweep between 5,000 Hz and 15,000 Hz.

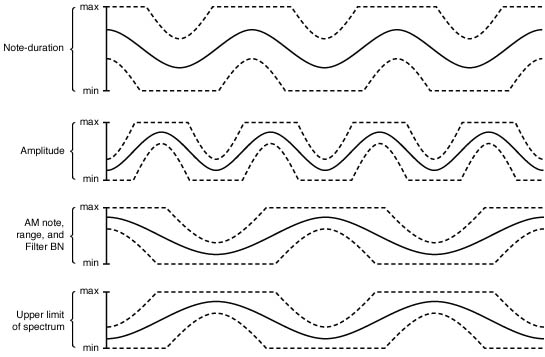
Figure 4.14  James Tenney’s "Phases," one of the earliest and still most interesting pieces of computer-assisted composition. The pictures above are his "notes" for the piece, which constitute a kind of score.

Tenney made use of some simple modulation trajectories to control timbral parameters over time (like amplitude modulation rate, spectral upper limit, note-duration, and so on). By simply coding these functions in the computer and linking the output to the synthesis engine, Tenney was able to realize a number of highly original works in which he controlled the overall, large-scale process, but the micro-structure was largely determined by the computer making use of his curves.

"Phases" was released on an Artifact CD of James Tenney’s computer music.