Chapter 2: The Digital Representation of Sound,
Part Two: Playing by the Numbers

Section 2.3: Sampling Theory

So now we know that we need to sample a continuous waveform to represent it digitally. We also know that the faster we sample it, the better. But this is still a little vague. How often do we need to sample a waveform in order to achieve a good representation of it?

The answer to this question is given by the Nyquist sampling theorem, which states that to well represent a signal, the sampling rate (or sampling frequency—not to be confused with the frequency content of the sound) needs to be at least twice the highest frequency contained in the sound of the signal.

For example, look back at our time-frequency picture in Figure 2.3 from Section 2.1. It looks like it only contains frequencies up to 8,000 Hz. If this were the case, we would need to sample the sound at a rate of 16,000 Hz (16 kHz) in order to accurately reproduce the sound. That is, we would need to take sound bites (bytes?!) 16,000 times a second.

In the next chapter, when we talk about representing sounds in the frequency domain (as a combination of various amplitude levels of frequency components, which change over time) rather than in the time domain (as a numerical list of sample values of amplitudes), we’ll learn a lot more about the ramifications of the Nyquist theorem for digital sound. But for our current purposes, just remember that since the human ear only responds to sounds up to about 20,000 Hz, we need to sample sounds at least 40,000 times a second, or at a rate of 40,000 Hz, to represent these sounds for human consumption. You may be wondering why we even need to represent sonic frequencies that high (when the piano, for instance, only goes up to the high 4,000 Hz range). The answer is timbral, particularly spectral. Remember that we saw in Section 1.4 that those higher frequencies fill out the descriptive sonic information.

Xtra bit 2.1
Free sample:
a tonsorial tale

Just to review: we measure frequency in cycles per second (cps) or Hertz (Hz). The frequency range of human hearing is usually given as 20 Hz to 20,000 Hz, meaning that we can hear sounds in that range. Knowing that, if we decide that the highest frequency we’re interested in is 20 kHz, then according to the Nyquist theorem, we need a sampling rate of at least twice that frequency, or 40 kHz.

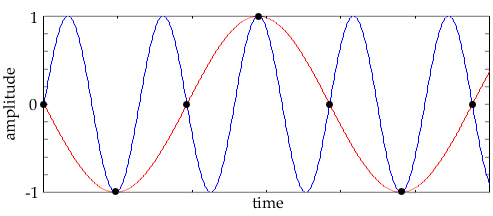
Figure 2.7  Undersampling: What happens if we sample too slowly for the frequencies we’re trying to represent?

We take samples (black dots) of a sine wave (in blue) at a certain interval (the sample rate). If the sine wave is changing too quickly (its frequency is too high), then we can’t grab enough information to reconstruct the waveform from our samples. The result is that the high-frequency waveform masquerades as a lower-frequency waveform (how sneaky!), or that the higher frequency is aliased to a lower frequency.

Applet 2.2
Oscillators

This applet demonstrates band-limited and non-band-limited waveforms.

Band-limited waveforms are those in which the synthesis method itself does not allow higher harmonics, or frequencies, than the sampling rate allows. It’s kind of like putting a governor on your car that doesn’t allow you to go past the speed limit. This technique can be useful in a lot of applications where one has absolutely no interest in the wonderful joy of listening to things like aliasing, foldover, and unwanted distortion.

Soundfile 2.1
Undersampling

Soundfile 2.1 demonstrates undersampling of the same sound source as Soundfile 2.2. In this example, the file was sampled at 1,024 samples per second. Note that the sound sounds "muddy" at a 1,024 sampling rate—that rate does not allow us any frequencies above about 500 Hz, which is sort of like sticking a large canvas bag over your head, and putting your fingers in your ears, while listening.

Soundfile 2.2
Standard sampling at 44,100 samples per second

Soundfile 2.2 was sampled at the standard 44,100 samples per second. This allows frequencies as high as around 22 kHz, which is well above our ear’s high-frequency range. In other words, it’s "good enough."

Figure 2.8  Picture of an undersampled waveform. This sound was sampled 512 times per second. This was way too slow.

Figure 2.9  This is the same sound file as above, but now sampled 44,100 (44.1 kHz) times per second. Much better.

Applet 2.3
Scrubber applet

Aliasing

The most common standard sampling rate for digital audio (the one used for CDs) is 44.1 kHz, giving us a Nyquist frequency (defined as half the sampling rate) of 22.05 kHz. If we use lower sampling rates, for example, 20 kHz, we can’t represent a sound whose frequency is above 10 kHz. In fact, if we try, we’ll get usually undesirable artifacts, called foldover or aliasing, in the signal.

In other words, if a sine wave is changing quickly, we would get the same set of samples that we would have obtained had we been taking samples from a sine wave of lower frequency! The effect of this is that the higher-frequency contributions now act as impostors of lower-frequency information. The effect of this is that there are extra, unanticipated, and new low-frequency contributions to the sound. Sometimes we can use this in cool, interesting ways, and other times it just messes up the original sound.

So in a sense, these impostors are aliases for the low frequencies, and we say that the result of our undersampling is an aliased waveform at a lower frequency.

Figure 2.10  Foldover aliasing. This picture shows what happens when we sweep a sine wave up past the Nyquist rate. It’s a picture in the frequency domain (which we haven’t talked about much yet), so what you’re seeing is the amplitude of specific component frequencies over time. The x-axis is frequency, the z-axis is amplitude, and the y-axis is time (read from back to front).

As the sine wave sweeps up into frequencies above the Nyquist frequency, an aliased wave (starting at 0 Hz and ending at 44,100 Hz over 10 seconds) is reflected below the Nyquist frequency of 22,050 Hz. The sound can be heard in Soundfile 2.3.

Soundfile 2.3
Chirping

Soundfile 2.3 is a 10-second soundfile sweeping a sine wave from 0 Hz to 44,100 Hz. Notice that the sound seems to disappear after it reaches the Nyquist rate of 22,050 Hz, but then it wraps around as aliased sound back into the audible domain.

Anti-Aliasing Filters

Fortunately it’s fairly easy to avoid aliasing—we simply make sure that the signal we’re recording doesn’t contain any frequencies above the Nyquist frequency. To accomplish this task, we use an anti-aliasing filter on the signal. Audio filtering is a technique that allows us to selectively keep or throw out certain frequencies in a sound—just as light filters (like ones you might use on a camera) only allow certain frequencies of light (colors) to pass. For now, just remember that a filter lets us color a sound by changing its frequency content.

An anti-aliasing filter is called a low-pass filter because it only allows frequencies below a certain cutoff frequency to pass. Anything above the cutoff frequency gets removed. By setting the cutoff frequency of the low-pass filter to the Nyquist frequency, we can throw out the offending frequencies (those high enough to cause aliasing) while retaining all of the lower frequencies that we want to record.

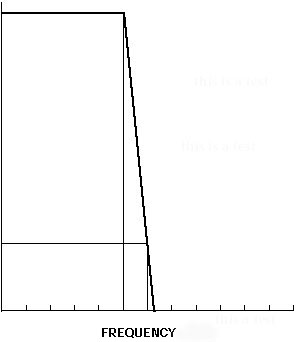
Figure 2.11  An anti-aliasing low-pass filter. Only the frequencies within the passband, which stops at the Nyquist frequency (and "rolls off" after that), are allowed to pass. This diagram is typical of the way we draw what is called the frequency response of a filter. It shows the amplitude that will come out of the filter in response to different frequencies (of the same amplitude).

Anti-aliasing filters can be analogized to coffee filters. The desired components (frequencies or liquid coffee) are preserved, while the filter (coffee filter or anti-aliasing filter) catches all the undesirable components (the coffee grounds or the frequencies that the system cannot handle).

Perfect anti-aliasing filters cannot be constructed, so we almost always get some aliasing error in an ADC→DAC conversion.

Anti-aliasing filters are a standard component in digital sound recording, so aliasing is not usually of serious concern to the average user or computer musician. But because many of the sounds in computer music are not recorded (and are instead created digitally inside the computer itself), it’s important to fully understand aliasing and the Nyquist theorem. There’s nothing to stop us from using a computer to create sounds with frequencies well above the Nyquist frequency. And while the computer has no problem dealing with such sounds as data, as soon as we mere humans want to actually hear those sounds (as opposed to just conceptualizing or imagining them), we need to deal with the physical realities of aliasing, the Nyquist theorem, and the analog-to-digital conversion process.