Week 6: Fractal Reflections; Room Simulation

Zion Canyon, Utah
click
here
for assignments from this class.
Fractal Reflections
Last week we discussed the use of fractal
techniques to generate various parameters of music. In this class, we
took a slightly different approach to using fractals than the "typical"
mapping onto pitch/frequency or rhythm, etc. (it's amazing how many
people think of algorithmic composition as working only in these two
domains). Fractal geometry is a very powerful way to represent natural
forms -- in fact, much of Mandelbrot's original investigations into
fractals dealt with issues of representing these forms; the coastline
of Britain, the size (area) of clouds, etc. His book is titled
The Fractal Geometry of Nature, after all!
As an example, the following image was generated entirely by fractal
techniques:

Not bad, eh?
[NOTE: If you would like to experiment with creating
your own fractal landsscapes, the
xmountains
package (complete with source code!) is a good place to start. We
showed this in class.]
The ability to capture essential features of landscapes leads to
interesting possibilities. One of my favorite sounds in the world
is the echoes and reflections that come from mountain and canyon
walls. Last summer, I stood for some time yelling things like
"Hey!" and clapping my hands while facing the Zion Canyon
walls shown in the picture at the top of the page. Lacking the
financial resources or time to conveniently travel to Utah
whenever I would like to re-create this sound, I of course turn to
the computer for assistance.
We can use fractal techniques to simulate this sound.
It is important to realize that an echo is basically nothing more than
a copy of a sound played at a later time. We already have the
ability to do this (play a sound at some future time) using the RTcmix
STEREO
instrument. All we need to do is generate the correct time-point data
to duplicate the reflections from a fractal boundary.
To do this, we need to write a program that will do this. The
essence of creating a fractal is the notion of recursion,
or applying the same operation over and over again -- but supplying
new data points (generated from the previous data points) at each
level of the recursion. For example, one of the most famous
fractals is a thing called the Koch Snowflake Curve. It is
created by taking a basic shape:
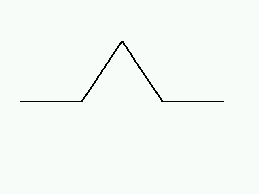
and then applying the procedure used to make the basic shape to each
sub-line of the basic shape (recursion level 1):
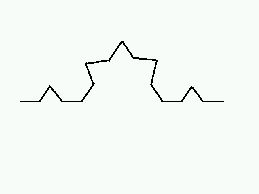
and then doing this again (recursion level 2):

and again and again... etc. Now suppose we came up with a procedure to
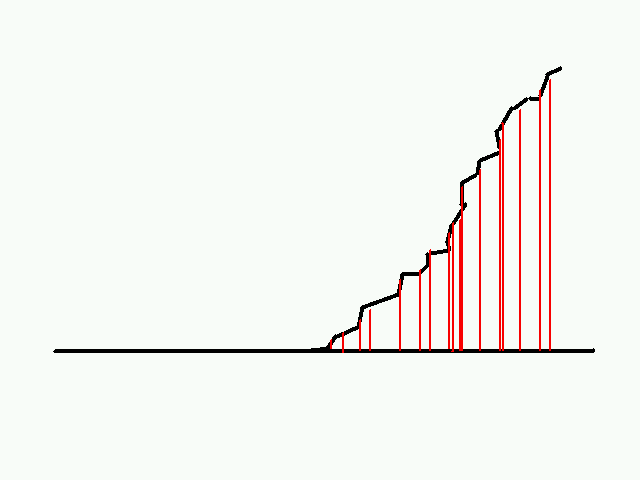
fractally generate a canyon-like wall, looking something like this:
 If we posit a hypothetical person standing a distance away from the
canyon, perhaps yelling "hey!", we can imagine that the sound will
travel from the source towards the virtual canyon wall:
If we posit a hypothetical person standing a distance away from the
canyon, perhaps yelling "hey!", we can imagine that the sound will
travel from the source towards the virtual canyon wall:
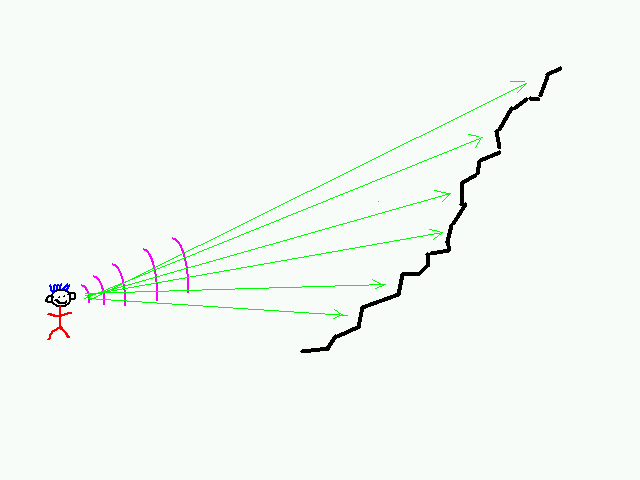 The sound waves would reflect from the canyon wall back towards the
person, each one delayed by the distance travelled to reach
a particular reflecting face of the wall:
The sound waves would reflect from the canyon wall back towards the
person, each one delayed by the distance travelled to reach
a particular reflecting face of the wall:
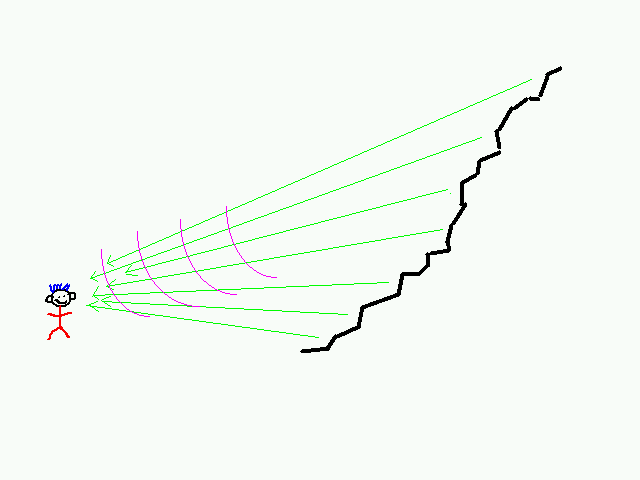 Now assuming that sound travels at about 1100 feet/second, we are
going to make several assumptions about our sonic model. Instead
of calculating the angles and exact path-lengths of every reflection,
we will map the fractal canyon wall down to a set of delay points
along the ground, essentially mapping the canyon wall from
2 dimensions to 1 dimension:
Now assuming that sound travels at about 1100 feet/second, we are
going to make several assumptions about our sonic model. Instead
of calculating the angles and exact path-lengths of every reflection,
we will map the fractal canyon wall down to a set of delay points
along the ground, essentially mapping the canyon wall from
2 dimensions to 1 dimension:
 The delay points would thus be generated by the (red) intersections
within the (green) time span below:
The delay points would thus be generated by the (red) intersections
within the (green) time span below:
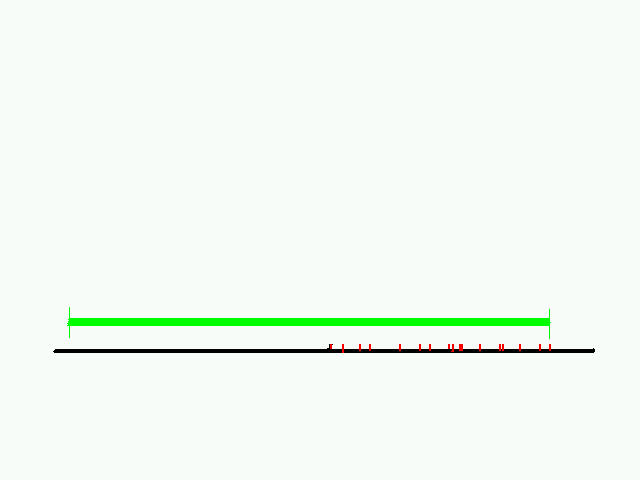 If we assume that the farthest point on the canyon wall is slightly less
than 550 feet from our source/listener person, and that the canyon
wall starts at some arbitrary distance from the source/listener
person less than this, then all we have to do is come up with a recursive
technique for dividing up points of time between 0 and 0.5 seconds.
Each point we generate will become a single delay, or a single
call to STEREO with a particular output skip parameter that
will generate that delay.
If we assume that the farthest point on the canyon wall is slightly less
than 550 feet from our source/listener person, and that the canyon
wall starts at some arbitrary distance from the source/listener
person less than this, then all we have to do is come up with a recursive
technique for dividing up points of time between 0 and 0.5 seconds.
Each point we generate will become a single delay, or a single
call to STEREO with a particular output skip parameter that
will generate that delay.
Although this sounds complicated, it is actually rather easy
to do. Suppose that we decide to generate fractal faces of our
canyon wall by deciding that each segment will have a face-point
(sound reflection point) at 70% of the "base" face. Calculating
the time delays is easy:
1. Take the time span 0.0 -- 0.5, multiply it by 0.7 to get
the first delay point (0.5 * 0.7 = 0.35).
2. Take the "cut" time spans (0.0 -- 0.35; 0.35 -- 0.5) and
multiply each one of these by 0.7 to get the second
set of time delay points (0.35 * 0.7 = 0.245;
(((0.5-035) * 0.7) + 0.35 = 0.455). [This is recursion level 1]
3. Take each of those "cut" time spans ( 0.0 -- 0.245; 0.245 -- 0.35;
0.35 -- 0.455; 0.455 -- 0.5) and apply the same procedure...[This
is recursion level 2]
4. etc.
Here's a crude graphical depiction of the above:
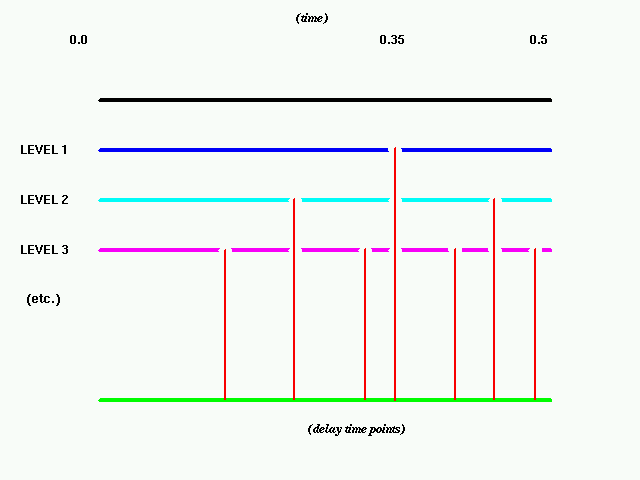
The code to do this is not complicated at all. Again, the main concept
to get around is the use of recursion in this procedure -- note that the
gendelays() function calls itself twice, with different pieces
of the "cuts" each time. We also check the level (in the following
code it is set at "4") to be sure that we don't continue cutting
into smaller and smaller pieces forever(level is passed as
one of the parameters for gendelays()).
The code (compile with a simple "cc"):
#include <stdio.h>
main()
{
void gendelays(float, float, int);
float start, end;
int level;
start = 0.0;
end = 0.5;
level = 0;
gendelays(start, end, level);
}
void gendelays(float st, float end, int level)
{
float mid;
mid = ((end-st) * 0.7) + st;
printf("STEREO(%f, 0.0, 3.0, 0.1, 0.5)\n", mid);
level = level+1;
if (level > 4) return;
gendelays(st, mid, level);
gendelays(mid, end, level);
}
If we collect the output of this program into a file, add the appropriate
rtsetparams() and rtinput() lines, we can run the resulting
scorefile and hear the reflections from the fractal wall!
As a matter of fact, you can hear them right now!:
Hey! -- recording of original soundfile (brad yelling "hey!")
fractal1 -- fractal-delayed version with number of recursion
levels set to 4
fractal2 -- fractal-delayed version with number of recursion
levels set to 7
Although this simulation of the reflection delay patterns is surprisingly
good, there is a regularity to it that signals "artificiality" to
the ear (believe it or not, this becomes more pronounced the more
levels of recursion there are (why?)). No natural form will
ever have an exact fractal dividing of 0.7 for every face -- instead
the recursive procedure slightly varies from one level to the next.
We can imitate this by adding a slight amount of randomness to the
time-points we generate, and using this randomness prior to subsequent
recursive calls so that it will be reflected in the overall fractal
structure that we generate. The change is very minor -- we take the
orginal version of the gendelays() function:
void gendelays(float st, float end, int level)
{
float mid;
mid = ((end-st) * 0.7) + st;
printf("STEREO(%f, 0.0, 3.0, 0.1, 0.5)\n", mid);
level = level+1;
if (level > 4) return;
gendelays(st, mid, level);
gendelays(mid, end, level);
}
and add one additional line of code, using the rrand()
function (returns a value between -1.0 and +1.0):
void gendelays(float st, float end, int level)
{
float mid;
mid = ((end-st) * 0.7) + st;
mid = mid + (rrand() * 0.01);
printf("STEREO(%f, 0.0, 3.0, 0.1, 0.5)\n", mid);
level = level+1;
if (level > 4) return;
gendelays(st, mid, level);
gendelays(mid, end, level);
}
Of course, because we've done this we will need to #include the
following line at the top of the file:
and compile it by saying: "cc -o fract2 fract2.c /musr/cmix/lib/randfuncs.o -lm"
(assuming of course that the file containing the code is "fract2.c").
The results of this version can be heard with this mp3 file:
randomized fractal -- soundfile generated using slight
amounts of randomness in the fractal procedure
A CSOUND Instrument
coming soon...
Room Simulation
Calculating reflections from a fractal boundary is very similar to
approaches used in simulating different room acoustics. Basically,
many of these approaches use a technique analogous to "ray tracing"
in creating models of light used for graphics. The trick is to
find the optimum reflection from th walls in a virtual room
you are modelling -- optimum being where the angle of incidence
is equal to the angle of reflection -- and to use the distance
to dictate delay poin.
More coming later...
Assignments:
1. Account for amplitude in the calculation of the delays (hint: the
amplitude of sound is inversely proportional to the square of the
distance travelled).
2. Use fractal techniques to control some other parameter of sound,
perhaps timbre-construction.
3. Account for three-dimenional "spatialization"; include several
different surfaces (and possibly reflective objects) (hint:
include the timing differences between ears of the listener).











