Two New Approaches to the Simulation of Acoustic Spaces
Brad Garton
Music Department, 703 Dodge Hall
Columbia University
New York, NY 10027
brad@woof.columbia.edu
ABSTRACT
The "traditional" models for room-simulation algorithms rely upon
idealized assumptions which greatly simplify acoustic reality. The
justification for these assumptions is to decrease to a manageable
level the complexity involved in simulating natural spaces. This paper
explores two algorithms where concerns for efficiency and computational
complexity were not major factors. The first algorithm uses fractal
techniques to generate delays intended to model the reflections of
sound from a complex surface (such as a canyon wall). The second algorithm
simulates the acoustic response characteristics of arbitrarily-shaped
rooms by modelling the action of "packets of air" contained within
the rooms.
A truly wonderful capability of digital synthesis and signal processing
is the ability to simulate an acoustic space. The creation of an auditory
ambience can be one of the most evocative tools a computer musician
has at his or her disposal. Much research has gone into designing
better and more efficient methods for producing the impression of
acoustic space, with the bulk of the research effort concentrated
on simulating large, indoor rooms. The "standard" paradigm for this
simulation is to synthesize the initial response of the room by modelling
the primary (and often secondary) wall reflections using a ray-tracing
approach, and then recreate the subsequent diffuse reflections with
a recirculating reverberator scheme. This method is quite good, both
in the fact that it captures most of the important acoustic cues used
to decode the aural experience of space, and also because the implementation
is relatively straightforward and fast (see [Moore, 1990] for a good
discussion of this technique). There are some limitations to the model,
however. It is difficult to simulate rooms of arbitrary shape and
size, or rooms with objects placed at locations which would interfere
with a spreading sound wavefront. It is also nearly impossible to
create the sensation of an outdoor space using the ray-tracing/diffusion
method.
The Fractal Reverberator -- Outdoor Spaces
While it seems extremely difficult in principle to simulate the sound
of "the outdoors" -- so much is dependent upon information about the
environment gained through other sense modalities -- it should be
possible to recreate the sound of certain specific outdoor features.
In particular, the sound of acoustic reflections from canyon or mountain
walls, or the diffuse sound of reverberation in a forest could be
modelled using discrete delay lines with delay times corresponding
to a reconstruction of the reflective surfaces present in the actual
outdoor environment (see figure 1).

If the delay line lengths were
based upon some physical system, it would represent an extreme case
of the ray-tracing approach, where every delay corresponded to a sound
waveform vector from a single reflective surface. By borrowing some
techniques from the graphical simulation of landscapes using fractal
algorithms [Mandelbrot, 1977], it is possible to greatly simplify
the calculation of the delay line lengths.
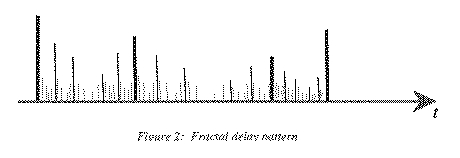
The basic algorithm for generating the delay lengths is straightforward:
simply take a pattern of delays
(with corresponding attenuations) and repeat it recursively within
the delay intervals of the original pattern (see figure 2). Used with
no modification of the original pattern in the recursing process,
this technique will yield a variety of interesting comb filter-like
effects. The pitch of the comb will be related to a common delay time
generated by the recursion. Rarely does "the outdoors" sound like
comb filters, however. If the pattern is modified during the recursion,
a variety of delay effects, including the effect of an outdoor space,
can be achieved.. The beauty of fractal algorithms is that they seem
to capture the undulations and indentations of natural surfaces with
a high degree of accuracy. Thus, realistic delays from a simulated
mountain wall or forest can be generated quite easily using this technique.
Direct Simulation of Room Acoustics
As good as the ray-tracing/diffusion model is for creating a room-like
ambience, it has some limitations. The ray-tracing technique used
to generate the initial room response characteristics is based upon
idealized assumptions about room geometry. Rooms which are constructed
as simple polygons (usually rectangles) make the computation of the
waveform vectors relatively simple. Any additional "features" in the
room greatly increase the complexity of the ray-tracing approach.
Also, because the initial reflections from the walls of the simulated
room are thought of as single vectors, it is practically impossible
to create a wall with varying acoustic properties (draperies, wall-hangings,
etc.).
The direct simulation approach allows for the design of rooms with
arbitrary shapes and varying acoustical characteristics. It is also
quite simple to insert objects with acoustic properties anywhere in
the room. The technique works by modelling the entire acoustic waveform
as it expands and reflects through the room. A room is thought of
as an array of nodes. Each node represents a "packet" of air. Sound
propagates through the room by passing samples through each node to
neighboring nodes in the direction of the wavefront travel (see figure
3). Every node delays the sound according to the width of the "packet"
represented by the node. Other attributes can by stored on the individual
node-objects, thus making it easy to create different acoustical features.
Sound sources and receivers can also be inserted as attributes of
particular node-objects.

Difficulties
If the grid for the nodes in the direct simulation model is regular
(as in figure 3), then the resulting sound will have a sharp resonance
corresponding to the comb filter created by the sound path delay of
each node. In this case, sound would always be delayed by a multiple
of the "unit" node delay. This effect can be eliminated by deforming
the node matrix or by randomizing the node pattern throughout the
room. Another solution is to make the nodes represent a packet of
air exactly one sample wide.
The problem with this second solution is the general problem with
both the fractal reverberator and the direct simulation room model.
Both are not 'efficient' in any sense of the word. The fractal reverberator
typically generates hundreds of taps on a delay line which must be
accessed for each sample computed. The direct room simulator requires
an enormous amount of computation. since every single node must be
updated for every sample. On a Sun 3/280 running with a Sky floating
point accelerator, a moderate-sized room required 50,000 cpu seconds
to generate one second of sound. It is doubtful that either of these
algorithms will see widespread use in the immediate future.
References
Moore, F. R., Elements of Computer Music, Prentis Hall, Englewood,
NJ, 1990.
Mandelbrot, B., The Fractal Geometry of Nature, W. H. Freeman and
Company, New York, 1977.



