Paper presented at the IMS 2022 conference in Athens, Greece on August 23, 2022

Bridging the Tonal/Atonal Dichotomy:

Some Principles of Pitch Organization Across the Border

Akira Takaoka
J.F. Oberlin University, Tokyo, Japan
Tokyo College of Music, Tokyo, Japan

TOC:

1. Introduction

2. POSITION-FINDING: Browne(1981), Butler(1989)

3. Stravinsky’s Choice of Pitch Materials

4. Issues of Current Atonal Theory

5. Analyses of Webern's Op. 27 and the Large-Scale Structure of "Liberame"

6. Conclusions: Some Principles of Atonal Pitch Organization

References

1. Introduction

The present study argues that:

• Both tonal and some atonal music use the same resources provided by the diatonic set.
  
  
• Some composers of atonal music such as Schoenberg, Stravinsky, and Webern deliberately chose pitch materials when they composed their atonal pieces so that they could make use of some properties of the diatonic set.

2. POSITION-FINDING (Browne 1981)

POSITION-FINDING: According to Browne (1981),

2.1. POSITION-FINDING in Tonal Music

 

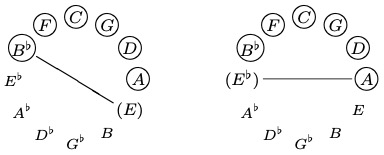
Example 2.4: Two possible POSITIONS up to the first beat of m. 3.

Psychologist David Butler elaborates on the idea of POSITION-FINDING and proposes what he calls the Intervallic Rivalry Model:

Intervallic Rivalry Model (Butler 1989):

Because of the "style-bound conventions," we initially find our POSITION in C scale on F but, with the E^♭ in m. 3, we find our POSITION in C scale on B^♭ to be a better candidate.

In addition, psychological experiments by Butler and Brown (1981, 53) demonstrate that,

 

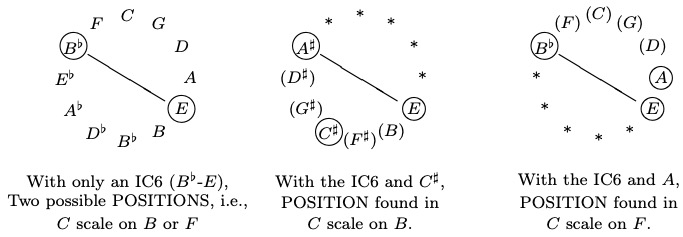
When we identify a diatonic set, since not all the seven members of the set have to be present, we must be able to find our POSITION in non-tonal contexts as well.

Working Hypothesis:

2.2. POSITION-FINDING in Some Atonal Music

 

• Without D^♭ in m. 3, we found our POSITION in C scale on F.
• Because of D^♭, or C^♯, in m. 3, the pc-set in m. 3 implies the D harmonic minor scale.

Is the way the pitches are organized in Schoenberg's Op. 11 so that we can carry out POSITION-FINDING just an accident or intentional?

3. Stravinsky’s Choice of Pitch Materials in His 12-Tone Compositions

3.1. Stravinsky’s Compositional Process of "Libera me" from Requiem Canticles

The compositional process of Stravinsky's 12-tone pieces:

When Stravinsky composed 12-tone pieces, he

Step 1: chose a tone row as a pair of unordered hexachords,

Step 2: derived subsets of the hexachords, and

Step 3: arranged the subsets to make harmonies.

At each step, he used not all available pc-sets but chose only some of them for his compositions.

In other words, he preferred some particular pc-sets to the others.

 

 

 

3.2. Stravinsky’s Choice of Tetrachords for "Libera me" from Requiem Canticles

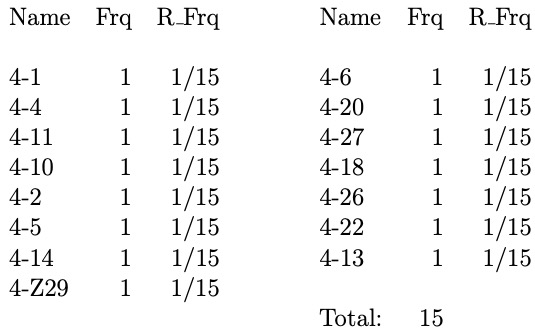
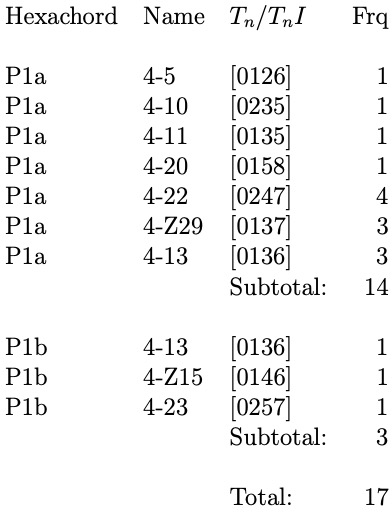
Stravinsky chose 12-tone rows as pairs of unordered hexachords first and derived pitch materials for harmonies, motives, and melodies.

Stravinsky chose the following two 12-tone rows for his Requiem Canticles:

 

 

At most ₆C₄ = 6!/(6 − 4)!4! = 15 different tetrachords can be derived from a single hexachord
(₆C₄ is sometimes denoted as C_{(6, 4)}, C_{6, 4}, or C 6 4 ).

 

 

• Since all the tetrachords have the same relative frequency, if randomly chosen, each of them has the same probability.
  
  
• As Example 3.8 shows, however, the Tn/TnI tetrachords Stravinsky derived from P1a for "Libera me" do not have the same frequencies.

 

• Since 14 tetrachords are derived from 6-Z40, the first half of P1, and the expected number of the frequency of each tetrachord is 14/15,
  
  
• χ² test (p=0.025) shows that Stravinsky’s choice of the tetrachordal subsets of 6-Z40 is biased, or intentional, at the 2.5% significance level.
  
  
• It follows that Stravinsky did not choose the tetrachords at random but preferred some, in particular, 4-22, 4-Z29, and 4-13, to the others.

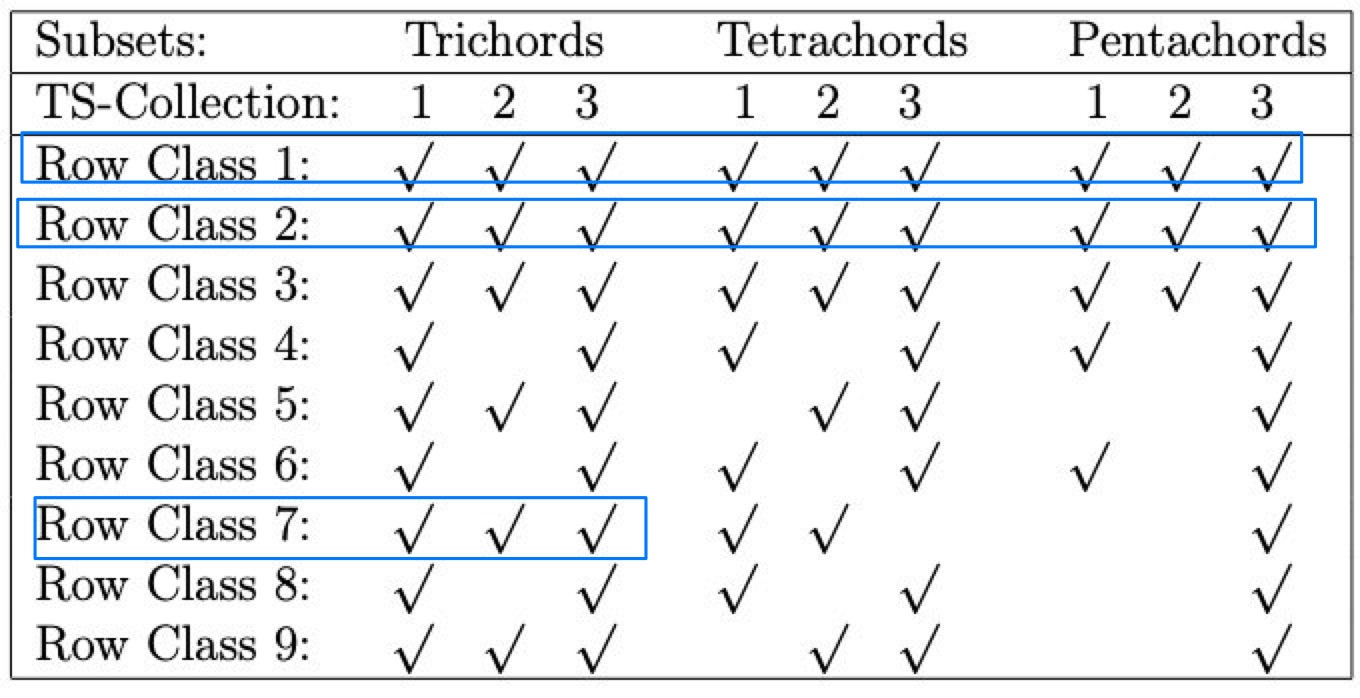
Tn/TnI types can be categorized into the following three Tritone-Sensitive Collections, TS-Collections for short, with respect to POSITION-FINDING:

We can carry out POSITION-FINDING in "Libera me" because most tetrachords chosen by Stravinsky are those of TS-Collection 1 and 2.

Next, we need to examine to what extent the TS-Collections are determining factors for phrase formation, melodic contours, and large-scale structures of atonal compositions.

But, before doing that, we need to discuss some methodological issues first.

4. Issues of Current Atonal Theory

4.1. Issues of Segmentation

We are now dealing with something unknown, unknown categories of musical entities that are characteristic of atonal music and equivalent to triads, scales, nonharmonic tones, functions, cadences, and so on in tonal music. Each style of music is characterized by its own categorization of musical entities.

I started with my personal impression of the way Schoenberg's piano piece is heard and hypothesized that we carry out POSITION-FINDING in atonal music as well as tonal one. And my whole arguments so far rely on that personal impression.

I'm quite aware that, for many music theorists, the way I'm handling the issues of atonal pitch organization seems too intuitive and too much relies on personal experiences.

I would like to defend the way I tackle the issues of atonal theory now. Let me start with issues of segmentation.

Segmentation (categorization into musical kinds)

"The procedure of determining which musical units of a composition are to be regarded as analytical objects. (Forte 1973, 83)"

"Atonal Kinds": analytical or compositional units and their relations characteristic of atonal music.

What we still don't know are those Atonal Kinds.

4.2. Issues of Similarity and Categorization

To find atonal kinds, many similarity criteria have been proposed by music theorists. They are based on the following assumptions:

"Similar" entities or relations share the same properties and hence belong to the same set and form a category, or a musical kind.

A musical kind can be defined by specifying the properties shared by its members.

It is a common practice in pc-set theory and transformational theory to define similarities with respect to shared properties such as the number of common pitch classes or interval classes and to classify transformations, set-classes, or their relations accordingly because it is assumed that those “similar” entities or relations should belong to the same set and form an atonal kind.

Forte (1977), for example, defines the following types of similarity relations:

For instance, if two pc-sets have the same cardinality and only one pitch class is different, they are called "maximally similar."

The assumptions above are not plausible, however, and all the similarity criteria proposed so far do not work for the following reasons:

Because issues of categorization and similarity have been discussed extensively in the fields of analytical philosophy and philosophy of science by philosophers such as Rudolf Carnap, Nelson Goodman, and W. v. O. Quine, let me outline what their arguments about categorization and similarity would be like if applied to current atonal theory.

1. Any two or more objects have some properties in common but they do not necessarily look similar to each other.

Consider, for example, the following three sets:

Assume:

Set A = {five computers},
Set B = {four books, one chocolate parfait},
Set C = {Palestrina, Bach, Ravel, Stravinsky, Kern}.

Then, sets A, B, and C are all members of the following superset F:

Superset F = {x | x is a set of size 5}

So, because the sizes of sets A, B, and C are all 5,
A, B, and C are members of the same superset F

But, although they share the same property and belong to the same superset F, sets A, B, and C are not similar to each other.

In other words,

ANY two or more objects have some properties in common and can be members of the same set no matter how "different" they are.

In addition,

2. Any Properties Can Be Put Together In Any Arbitrary Ways.

For example, the following is a set of creatures defined by the combination of two properties:

Set S = {x | Using_a_Double-Articulated_Language(x) ∧ Having_Six_Feet(x)}

These strange creatures share the same properties with human beings and six-foot insects.

So, if kinds are defined solely by properties, because they share property "Using_a_Double-Articulated_Language(x)," we find the creatures similar to human beings and both the strange creatures and human beings are members of the same category, or of the same kind of creatures.

Needless to say, we don't believe that the creatures and human beings are similar to each other or they are of the same kind.

Even if two or more different pc-sets or transformations share the same properties, they are not necessarily similar to each other for the same reason that the strange creatures and human beings are not similar to each other.

In short,

"Similarity cannot be equated with, or measured in terms of, possession of common characteristics" (Goodman 1972, 443). "The grouping of occurrences under a work or an experiment or an activity depends ... upon the possession of certain characteristics" (440; emphasis added).

And I believe that, in the case of the categorization of pitch materials of atonal music, those "certain characteristics are the tritone-sensitiveness.

"...the similarity notion [that is, categorization], starting in its innate phase, developing over the years in the light of accumulated experience, passing then from the intuitive phase into theoretical similarity. . . " (Quine 1969, 136ff ).

Therefore, as a theory develops, experience-based notions such as POSITION-FINDING will be replaced by more theoretically entrenched ones. Since my formulation of principles of atonal pitch organization is still in its infancy, it cannot help but rely on experience-based notions and categorization.

5. Analyses of Webern's Op. 27 and the Large-Scale Structure

5.1. Coordination of POSITION-FINDING, Melodic Contours, and Phrasing

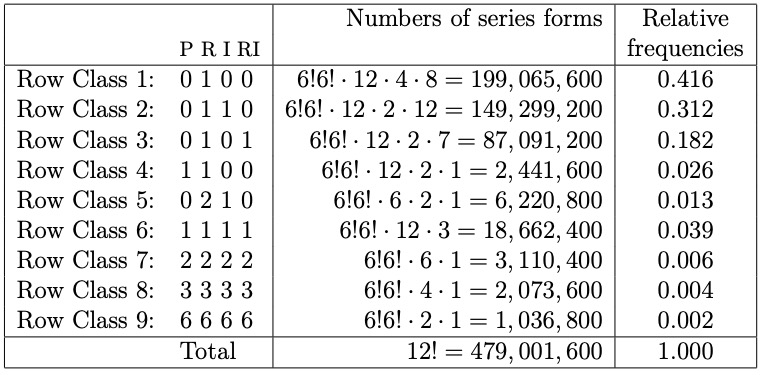
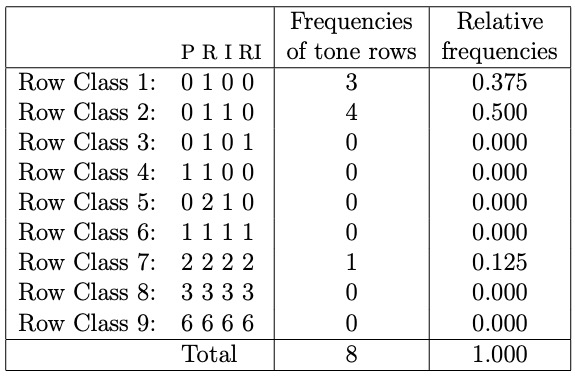
Webern's Piano Variation OP. 27 is in ternary form, ABA'. Section A consists of four phrases a-b-c-b'.

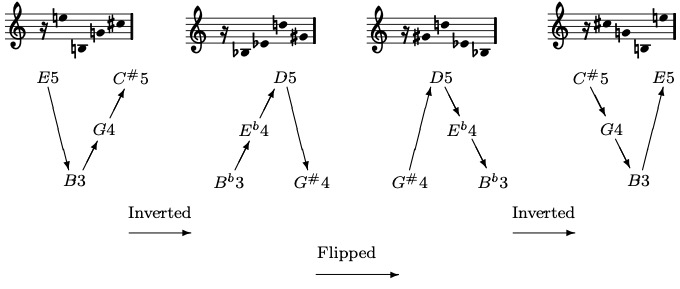
Each series form is stacked with its retrograde counterpart as shown in the following example:

For this piece, Webern chose a tone row. Two of the every consecutive three pitch classes form a tritone.

P0: R0:

The probability of the choice of the 12-tone rows for Webern's Op. 27

• Webern used every tone row with its retrograde series form.
• Every pitch-class appears strictly in the order of the combined tone rows.
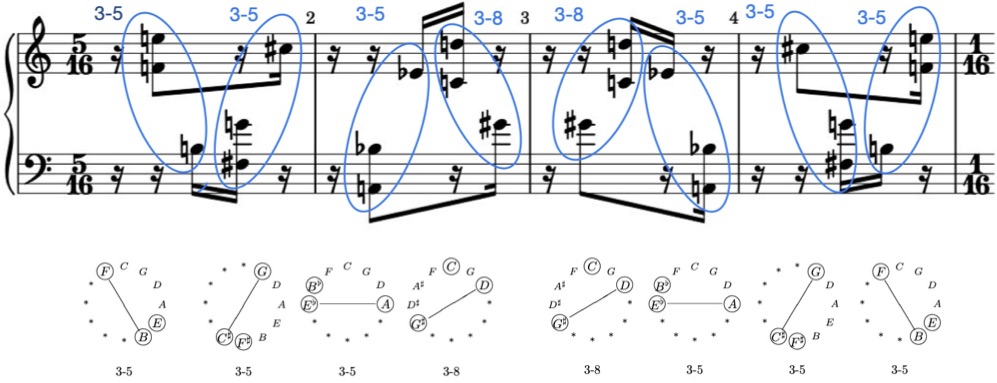
• Every motive in the first seven measures is a trichord.

The total number of the 12-tone rows that satisfy these conditions is:

₁₂C₄ = 495
495 * 6 * 4 = 11880

Thus the probability that such tone rows are chosen randomly is:

11880 / 12! = 0.0000248

In other words, if you pick a tone row randomly, you get such a tone row approximately once every 50,000 trials.

So, it's quite likely that Webern deliberately chose the tone row so that he could arrange a series of trichords each of which consists of one tritone and another single pitch class.

The first two measures:

 
             
             

5.2. A Large-Scale Structure with POSITION-FINDING

Resources provided by the diatonic set are utilized in not only local events but also the large-scale construction of an entire movement or piece of some atonal music.

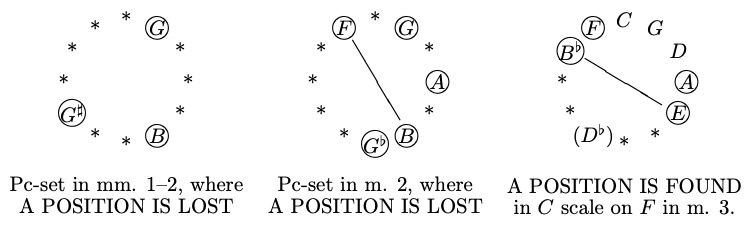
In m. 6 in Example 5.5 below, the two consecutive diminished 7th chords, with which POSITION is LOST, make the subsequent progression from the dominant pedal to the tonic even more convincing.

 

J.S. Bach. "Prelude" in C major. Das Wohltemperirte Clavier I, BWV 846, presented in four-bar hypermeter.

Example: 5.5: States of POSITION; S(uggested), C(onfirmed), F(ound), or L(ost); and transitions

5.3. A Large-Scale Structure in Stravinsky's "Libera me"

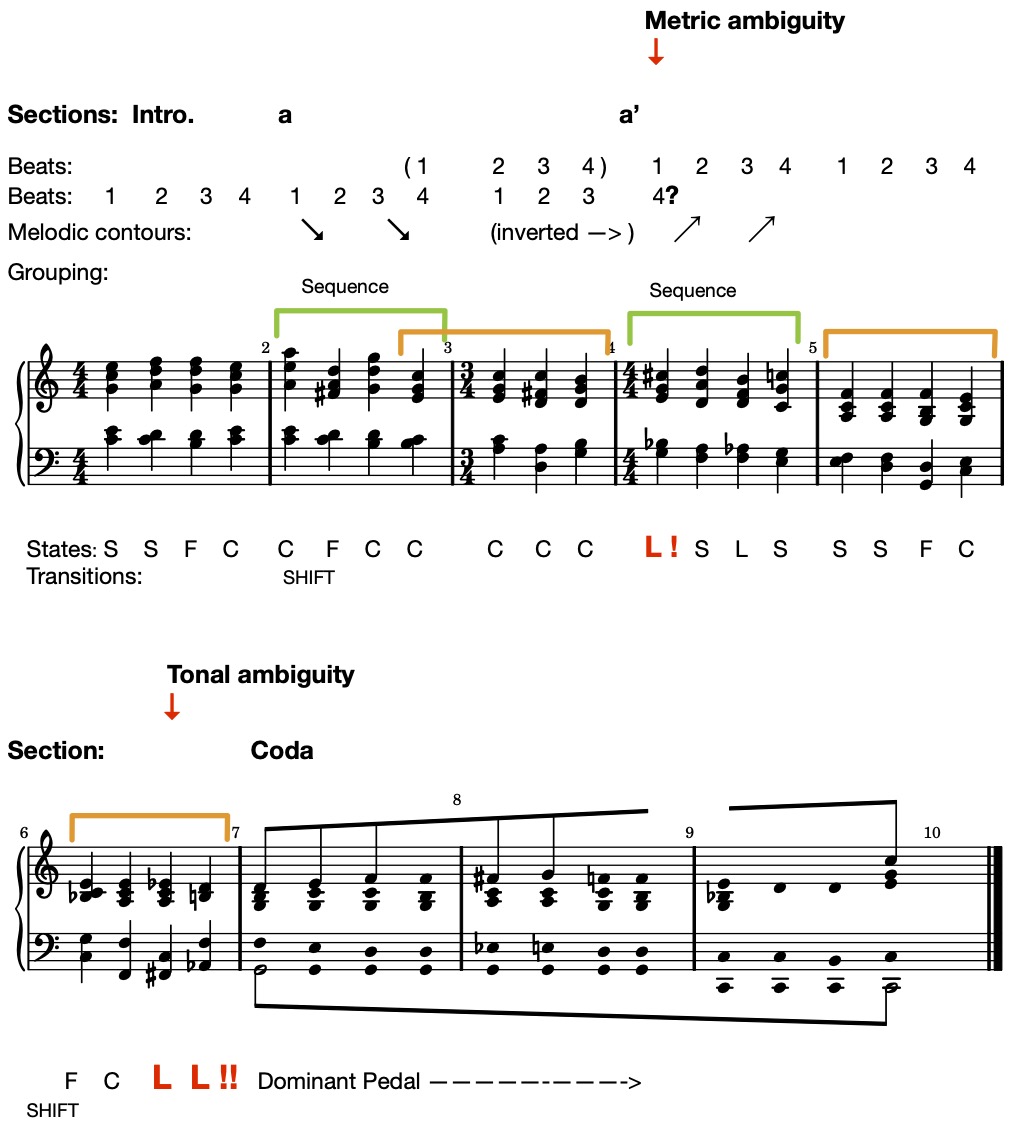
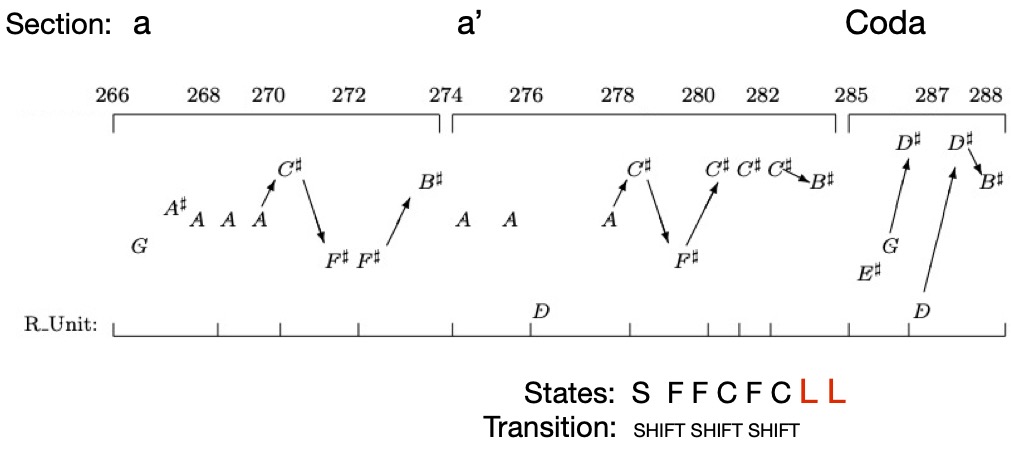
A similar large-scale structure in terms of POSITION-FINDING is found at the end of Section a' from Stravinsky's "Libera me"

 

In the entire movement of "Libera me," LOST POSITIONS are located at the end of Section a' preceding the Coda section shown below:

 

 

Example 5.8: Stravinsky, Section a' and Coda from "Libera me"

• The rhythmic compression happens towards the end of section a', the compression adds more tension to the closing of the section than the preceding one and hence prompts the following coda section to be introduced.


• The consecutive SHIFTS by T₇ in mm. 279-80 also increase tension and move towards the climax at the end of section a'.


• In mm. 283-4, pc-set 4-5, a non-subset of the diatonic set, makes us lose our POSITION and the subsequent Coda section sound even more convincing.

It seems as if, for these tonal and atonal compositions, J.S. Bach and Stravinsky used the same archetypal plot. One of our favorite plots is recounted as a new story with new pitch materials so that we can appreciate it from a fresh perspective.

6. Conclusions: Some Principles of Atonal Pitch Organization

Some Atonal Kinds

6.1. TS-Collections

• TS-Collection 1:
        Subsets of the diatonic set without a tritone
  
  
• TS-Collection 2:
        Subsets of the diatonic set with a tritone
  
  
• TS-Collection 3:
        Non-subsets of the diatonic set

 

6.2. States and Transitions of POSITIONS

Four States of POSITION:

A POSITION is
      1. FOUND,
      2. CONFIRMED,
      3. SUGGESTED, or
      4. LOST.

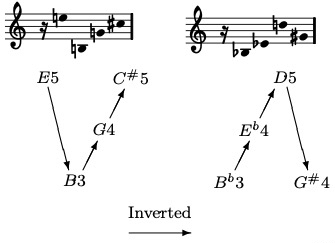
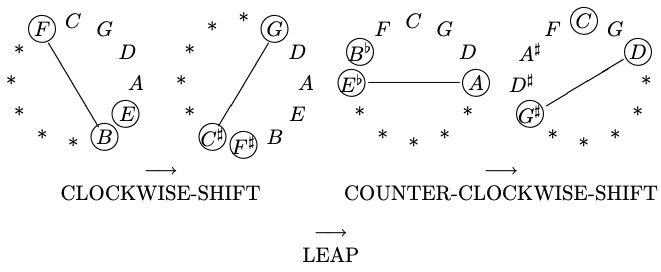
Two Transitions of POSITION:

POSITIONS
      1. SHIFT, or
      2. LEAP.

Conclusions::

References

Brown, Helen. 1988. "The Interplay of Set Content and Temporal Context in a Functional Theory of Tonality Perception." Music Perception 5 (3): 219–50. Browne, Richmond. 1981. "Tonal Implications of the Diatonic Set." In Theory Only 5 (6–7): 3–21.

Butler, David. 1989. "Describing the Perception of Tonality in Music: A Critique of the Tonal Hierarchy Theory and a Proposal for a Theory of Intervallic Rivalry." Music Perception 6 (3): 219–42.

Butler, David, and Helen Brown. 1981. "Diatonic Trichords as Minimal Tonal Cue-Cells." In Theory Only 5 (6–7): 39–55.

____ . 1984. "Tonal Structure versus Function: Studies of the Recognition of Harmonic Motion." Music Perception 2 (1): 6–24.

Forte, Allen. 1973. The Structure of Atonal Music. New Haven: Yale University Press.

Gibson, D. B., Jr. 1986. "The Aural Perception of Nontraditional Chords in Selected Theoretical Relationships: A Computer-Generated Experiment." Journal of Research in Music Education 34 (1): 5–23.

____. 1988. "The Aural Perception of Similarity in Nontraditional Chords Related by Octave Equivalence." Journal of Research in Music Education 36 (1): 5–17.

____. 1993. "The Effects of Pitch and Pitch-Class Content on the Aural Perception of Dissimilarity in Complementary Hexachords." Psychomusicology 12 (1): 58–72.

Goodman, Nelson. 1972. "Seven Strictures on Similarity." In Problems and Projects, 13–23. Indianapolis and New York: The Bobbs-Merrill Company. Also in Douglas and Hull (1992).

____. 1983. "The New Riddle of Induction." In Fact, Fiction, and Forecast, 4th ed, 59–83. Cambridge, Mass.: Harvard University Press.

Isaacson, Eric J. 1990. "Similarity of Interval-Class Content between Pitch-Class Sets: the IcVSIM Relation." Journal of Music Theory 34 (1): 1–28.

Kramer, Jonathan D. 1988. The Time of Music. New York: Schirmer Books.

Lakoff, George, and Mark Johnson. 1980. Metaphors We Live by. Chicago and London: The University of Chicago Press.

Lerdahl, Fred. 1989. "Atonal Prolongational Structure." Contemporary Music Review 4:65–87.

Lord, Charles H. 1981. "Intervallic Similarity Relations in Atonal Set Analysis." Journal of Music Theory 25:91–111.

Meyer, Leonard B. 1989. Style and Music: Theory, History, and Ideology. Philadelphia: University of Pennsylvania Press.

Morris, Robert. 1979–80. "A Similarity Index for Pitch-Class Sets." Perspectives of New Music 18:445–60.

Narmour, Eugene. 1990. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. Chicago and London: The University of Chicago Press.

____. 1992. The Analysis and Cognition of Melodic Complexity: The Implication-Realization Model. Chicago and London: The University of Chicago Press.

Perle, George. 1977. Twelve-Tone Tonality. Berkeley: University of California Press.

Quine, Willard van Orman. 1969. "Natural Kinds." Ontological Relativity and Other Essays, 114–38. New York: Columbia University Press.

Rosch, Eleanor. 1973. "On the Internal Structure of Perceptual and Semantic Categories." Cognitive Development and Acquisition of Language, edited by Timothy E. Moore, 111–44. New York: Academic Press.

____. 1978. "Principles of Categorization." Cognition and Categorization, edited by Eleanor Rosch and Barbara B. Lloyd, 28–48. Hillsdale, New Jersey: Lawrence Erlbaum Associates.

____. 1983. "Prototype Classification and Logical Classification: The Two Systems." New Trends in Conceptual Representation: Challenges to Piaget’s Theory?, edited by Ellin Kofsky Scholnick, 73–86. Hillsdale, New Jersey: Lawrence Erlbaum Associates.

Rosch, Eleanor, and Carolyn B. Mervis. 1975. "Family Resemblances: Studies in the Internal Structure of Categories." Cognitive Psychology, no. 7:573–605.

Tversky, Amos, and Itamar Gati. 1978. "Studies of Similarity." Cognition and Categorization, edited by Eleanor Rosch and Barbara B. Lloyd, 81–98. Hillsdale, New Jersey: Lawrence Erlbaum Associates.